Kelly on How Far Can You See in an Orchard?

Well, how far can you see?

In this Prime Time Theorem, we pose a question that everyone has thought about deeply: If you stood in the center of a mathematical orchard, how far out would you be able to see without your line of sight being blocked by a tree?

Consider the following diagram, with trees (circles) of radius $0\leq r\leq 0.5$, centered at the unit lattice points.

Figure 1. A Mathematics Apple Orchard

To make some initial attempts, we can simplify our problem down to just the point centers of every tree:

• If we first consider the space excluding the centers of the trees, we simply get the infinite-area'd coordinate plane, except with holes at every ordered pair of integers. So this doesn't work.
• Perhaps if we introduced a constraint, such as not allowing there to be ``holes" in our area, then we would get a slightly more reasonable answer. We can still create a space of infinite area by simply ``weaving around" the coordinate points.
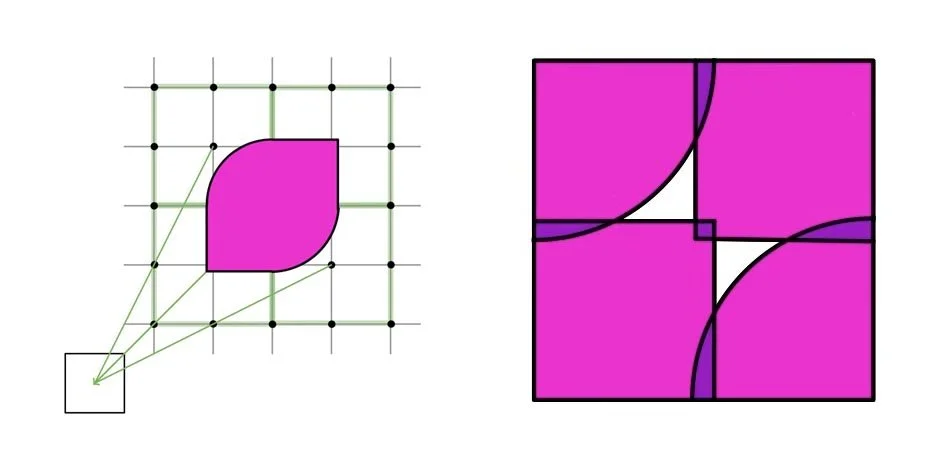
• Okay fine. Let's try something even more restricting. Consider a convex region that contains no lattice point other than $(0, 0)$. We define a \textbf{convex region} as such: For any two points in a convex region $R$, the line drawn between them is also in $R$. However, as Alex so cleverly noticed, we can draw a trapezoid that has infinite area, as shown in Figure \ref{Trapezoid}.

Figure 2: Alex's brilliant observation

2. There are theorems for this?

Next, we introduce a theorem proved by mathematician, Hermann Minkowski (1864-1909), fittingly called $\textbf{Minkowski's Theorem}$.

If a region $R$ is convex, contains $(0, 0)$, has an area greater than 4, and is centrally symmetric, then $R$ contains a lattice point other than $(0, 0)$.

Perhaps the only term that may be unfamiliar is \textbf{``Centrally Symmetric."} We define as the following: If a centrally symmetric region $R$ contains $(a, b), a, b\in \mathbb{R}$, then $(-a, -b)\in R$. In other words, the figure is symmetric with respect to a $180\degree$ rotation about the origin.

$$\textit{Proof:}$$ Consider any centrally symmetric figure of area greater than 4, such as this random example drawn by yours truly:

Figure 3: A beautiful convex, centrally symmetric region of area $>4$ in its natural habitat

Figure 4: The “Overlapping” Process

3. Applications

Now let's see what applications this elegant theorem has. Consider the following theorem.

If $\alpha$ is irrational, then there exist infinitely many $p, q\in \mathbb{Z}$ such that $|\alpha-\frac{p}{q}|<\frac{1}{q^2}$

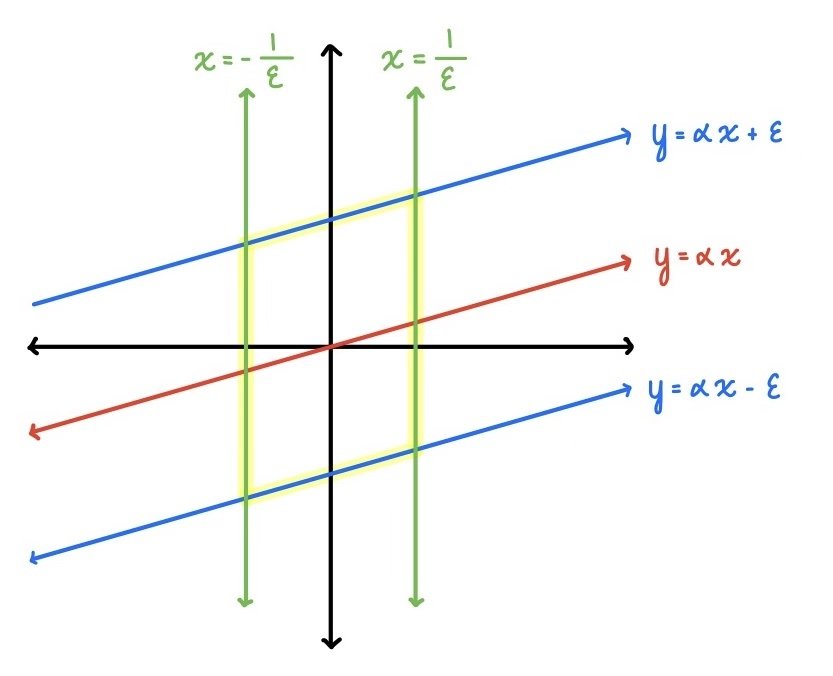
$\textif{Proof:}$ Consider the parallelogram bounded by the lines, $y=\alpha x+\epsilon, y=\alpha x-\epsilon, x=\frac{1}{\epsilon}, x=-\frac{1}{\epsilon}$.

Figure 5: Bounded Region

This parallelogram has area 4, so Minkowski's Theorem tells us that there is a nontrivial solution in $\mathbb{Z}^2$, and this concludes our proof.

Even with such a simple problem, we can create so many fascinating theorems and conjectures. This was an entertaining first Prime Time Theorem, one of many to come.